Гидростатическое давление
Гидростатическое давление жидкого тела — это сила, действующая на единицу площади. Средняя величина гидростатического давления определяется отношением силы, нормальной к поверхности, на которую она действует, к площади этой поверхности:
где F — нормальная сила, действующая на поверхность А, Н; А — площадь поверхности, на которую действует сила, м2; р — гидростатическое давление, Па.
Уравнение (9.3) описывает также давление в точке неподвижного жидкого тела.
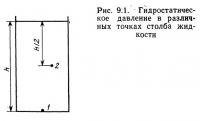
С помощью уравнения (9.3) можно определить давление на дне резервуара. Изображенный на рис. 9.1 резервуар наполнен жидкостью с удельным весом γ. Высота столба жидкости h, площадь поперечного сечения А. Давление.в точке 1 определяется уравнением (9.3). Сила, действующая на дно резервуара, равна произведению удельного веса жидкости у на ее объем:
Объем может быть получен умножением площади поперечного сечения столба жидкости А на его высоту h. Подстановка этих величин в формулу (9.4) дает
На основании уравнений (9.5) и (9.3) можно получить следующее выражение для величины давления в нижней точке столба жидкости:
После соответствующего сокращения уравнение (9.6) приобретает вид
Поскольку давление — это сила, приложенная к единице площади, площадью поперечного сечения можно пренебречь.
По уравнению (9.7) можно определить давление в любой точке столба жидкости. Оно будет равно произведению удельного веса жидкости на высоту столба жидкости над рассматриваемой точкой. Так, давление в точке 2 (см. рис. 9.1.)
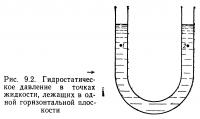
С помощью уравнения (9.7) можно показать, что во всех точках жидкости, лежащих в одной горизонтальной плоскости, давление одинаково. Если бы это было не так, жидкость потекла бы в сторону меньшего давления вместо того, чтобы занять такое положение, какое она занимает в сосуде, показанном, например, на рис. 9.2. Это действительно так, поскольку жидкости не могут оказывать сопротивление срезывающей силе и любая неуравновешенная сила приводит их в движение.
Абсолютное и избыточное (манометрическое) давление
Применительно к давлению, так же как и к температуре, берут за основу две критические точки отсчета. Для температурной шкалы это температура замерзания воды (0°С) и температура, при которой прекращается движение молекул — абсолютный нуль. Критические точки отсчета давления — это абсолютное нулевое давление (полный вакуум) и атмосферное давление. Соответствующие зависимости представлены на рис. 9.3. Стандартное атмосферное давление — это давление, соответствующее определенным стандартным условиям, которые принимаются при теоретических исследованиях газов. Давление, представляющее собой разность между абсолютным ра и манометрическим рм давлением, приблизительно равно стандартному атмосферному давлению. Уравнение для определения манометрического давления можно записать следующим образом:
Действительное атмосферное давление рд в зависимости от места измерения может быть больше или меньше стандартного атмосферного давления. Однако, если давление измеряется на уровне моря, оно почти всегда меньше стандартного атмосферного давления. Абсолютное давление всегда положительное. Избыточное манометрическое давление бывает либо положительным, либо отрицательным — вакуумметрическим давлением.
Приборы для измерения давления
Для измерения манометрического давления применяют различные приборы. Наиболее распространенные из них — манометры и трубки Бурдона. Ниже рассмотрены только манометры.
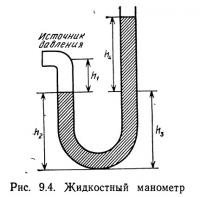
Манометр представляет собой трубку из стекла, пластмассы или другого материала, наполненную жидкостью. Один конец трубки присоединяется к сосуду, в котором необходимо измерить давление, а другой остается открытым, т. е. соединен с атмосферой. На рис. 9.4 показано устройство простейшего манометра. Давление, оказываемое на жидкость в одном из колен U-образной трубки, заставляет уровень жидкости в другом колене сместиться на величину, соответствующую давлению столба жидкости, высота* которого определяется разностью между приложенным давлением и атмосферным.
С помощью манометра измеряется разность между приложенным давлением и атмосферным. Это легко показать, если просуммировать все значения давлений вдоль манометрической трубки, начиная от приложенного давления и кончая атмосферным. Приложенное давление — величина неизвестная, его можно обозначить ps. Во всех точках, лежащих в горизонтальном сечении вдоль поверхности раздела жидкостей, давление будет одинаковым. В соответствии с уравнением (9.7) γ1h1 = p1. Аналогично
Однако согласно уравнению (9.4)
Следовательно, уравнение (9.10) можно записать следующим образом:
Правое колено U-образной трубки (см. рис. 9.4) соединено с атмосферой. Давление атмосферы на свободную поверхность жидкости в этом колене равно 1·105 Па, манометрическое давление равно нулю. Манометр измеряет разность давлений, в данном случае это разность между ps и атмосферным давлением. Таким образом, давление, полученное решением уравнения (9.12) относительно неизвестной величины ps, и будет манометрическим давлением.
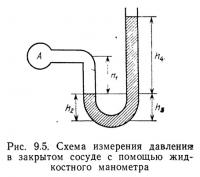
Пример 9.1. Определить манометрическое и абсолютное давление в сосуде А (рис. 9.5), если h1=3 м; h2=h3=2 м; h4=6 м.
Жидкость 1 — масло (удельный вес 0,9), жидкость 2 — вода (удельный вес 1). Удельный вес воды равен 9800 Н/м3.
Решение. Удельный вес масла можно представить как удельный вес воды, умноженный на коэффициент удельного веса масла (УВ):
Приравнивания давления, действующие в обоих коленах U-образной трубки, можно записать
Однако h2=h3, и если учесть, что оба колена заполнены одинаковой жидкостью, то уравнение (9.14) можно переписать в виде
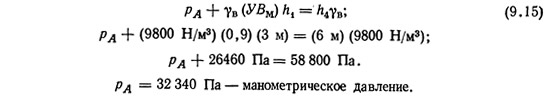
Абсолютное давление = рм+стандартное атмосферное давление.
Абсолютное давление = 32340 Па + 10000 Па = 42340 Па.
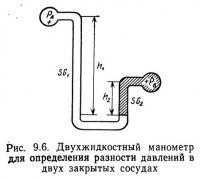
Пример 9.2. Определить манометрическое давление в сосуде В (рис. 9.6), если рА=3·105 Па; УВ1=1; УВ2=13,6; h1=3 м; h2=1 м.
Решение.
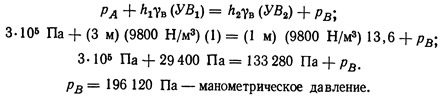
Расчет цилиндрических сосудов на разрыв
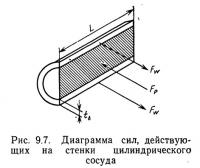
Цилиндрические сосуды, к числу которых можно отнести трубопроводы и резервуары, при эксплуатации испытывают значительные внутренние давления. В связи с этим необходимо знать максимально допустимое давление для того или иного трубопровода или резервуара. В инженерной практике пользуются формулой, устанавливающей зависимость между внутренним давлением в сосуде и напряжением, возникающем в стенках сосуда под действием этого давления. Найденное таким образом напряжение сравнивают с напряжением максимально допустимым для материала, из которого изготовлен сосуд. Если допустимое напряжение превышает расчетное, сосуд должен выдержать предполагаемое внутреннее давление. В противном случае неизбежна авария.
На рис. 9.7 схематически изображена зависимость между внутренним давлением, которое испытывает цилиндр, и напряжением, возникающим в его стенках под действием этого давления. На схеме изображены силы, действующие перпендикулярно плоскости продольного сечения цилиндра. Сила Fp — это сила давления жидкости, которая может быть рассчитана как произведение внутреннего давления на площадь поверхности, испытывающей действие этого давления:
где L — длина сечения; D — диаметр цилиндра; р — внутреннее давление.
Стенки цилиндра оказывают сопротивление давлению 'жидкости. Но поскольку в сечение, показанное на рис. 9.7, попадают два продольных разреза стенки цилиндра, уравнение равновесия сил выглядит следующим образом:
где Fw — сила, приложенная к поверхности продольного сечения стенки цилиндра.
Сила, возникающая в стенке, цилиндра, равна произведению напряжения растяжения на площадь продольного сечения стенки:
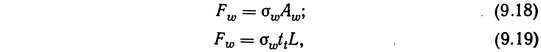
где tt — толщина стенки.
На основании уравнений (9.16), (9.17) и (9.19) можно записать
Решение этого уравнения дает следующее выражение для напряжения:
Уравнение (9.21) устанавливает зависимость между напряжением, возникающем в стенке цилиндрического сосуда, давлением жидкости в сосуде, толщиной стенок и диаметром сосуда. Данные о величинах допустимых напряжений для различных материалов приведены в табл. 9.1.

С помощью уравнения (9.21) можно определить величину напряжения, развивающегося в стенке цилиндрического сосуда при максимальном предполагаемом давлении. Однако при эксплуатации в трубопроводах могут возникать скачки давления, значительно превышающие максимальное давление. Приведенные в табл. 9.1 данные — это средние значения для различных материалов. Действительные значения допустимых напряжений для того или иного трубопровода или стенки резервуара могут в зависимости от условий эксплуатации быть несколько выше или ниже средних значений. Эти отклонения учитываются при проектировании коэффициентом безопасности или запасом прочности, который представляет собой отношение допустимого напряжения к действительной величине напряжения, возникающего в стенках сосудов в процессе эксплуатации:
Для большинства водопроводных систем запас прочности принимают равным 2. Величина запаса прочности для резервуаров и других сосудов колеблется в довольно широких пределах — от 1,5 до 5 в зависимости от длины трубопровода, характера возможных разрушений и других факторов.
С учетом запаса прочности уравнение для определения напряжения может быть записано в виде
где σA — допустимое напряжение материала.
Обычно данные о максимально допустимых давлениях, выдерживаемых трубопроводами, предоставляются фирмами-изготовителями. В тех случаях, когда эти данные отсутствуют, можно пользоваться уравнениями (9.21) и (9.22).
Пример 9.3. Определить допустимое рабочее давление для трубопровода номинальным диаметром 5,08 см, выполненного из поливинилхлорида марки 80 по американскому стандарту. Принятый запас прочности равен 2. Внутренний диаметр (ВД) трубы номинальным диаметром 5,08 см составляет 4,93 см, а наружный диаметр (НД) — 6,03 см.
Толщина стенки трубопровода (НД—ВД)/2=tt;
По табл. 9.1. выбираем допустимое напряжение для полихлорвинила, равное 48 МПа.
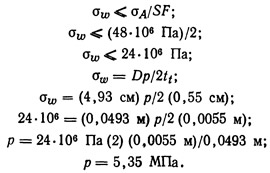
Другие вопросы гидростатики, такие, например, как методика определения сил давления на поверхность погруженного тела и центра давления, расчет сил, действующих на плотины и перемычки, также могут представлять интерес для специалистов, занимающихся разведением водных организмов. Однако в этой главе рассматриваются только те вопросы гидростатики, которые имеют непосредственное отношение к инженерным аспектам аквакультуры. Специалисты, интересующиеся вопросами гидростатики, не вошедшими в настоящую книгу, могут обратиться к соответствующей литературе, например к монографии Стритера (Streeter, 1962), Кинга и др. (King et al., 1948).